Large-scale Electronic Structure Theory and Methodology
“The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble. It therefore becomes desirable that approximate practical methods of applying quantum mechanics should be developed, which can lead to an explanation of the main features of complex atomic systems without too much computation.” – Paul Dirac, Quantum mechanics of many-electron systems (1929)
- Why Orbital Free Density Functional Theory (OF-DFT)
- It can simulate millons atom with 1 CPU
- 100+ millions of atoms by parallel computing
- Orbital-Free Density Functional Theory (OF-DFT)
- Kinetic Energy Density Functionals (KEDFs)
- Local pseudopotentials (LPP)
- OF-DFT solver
- Density Embedding/Subsystem Density Functional Theory (sDFT)
- Nonlocal sDFT
- Nonadditive KEDFs
- Deorbitalized Meta-GGA exchnage-correlation functionals
Subsystem DFT Beyond GGA Functionals (eQE2)
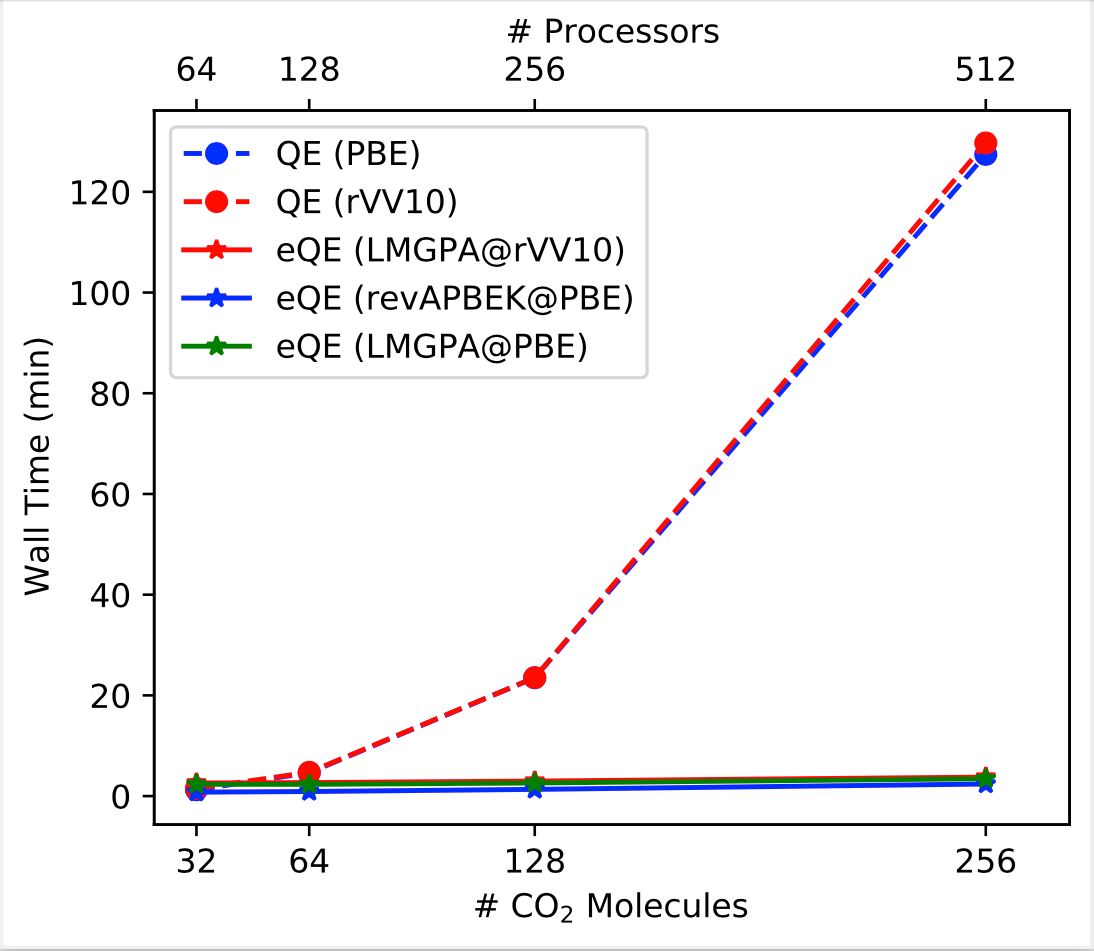
By adopting a divide-and-conquer strategy, subsystem-DFT (sDFT) can dramatically reduce the computational cost of large-scale electronic structure calculations. The key ingredients of sDFT are the nonadditive kinetic energy and exchange-correlation functionals which dominate it’s accuracy. Even though, semilocal nonadditive functionals find a broad range of applications, their accuracy is somewhat limited especially for those systems where achieving balance between exchange-correlation interactions on one side and nonadditive kinetic energy on the other is crucial. In eQE 2.0, we improve dramatically the accuracy of sDFT simulations by (1) implementing nonlocal nonadditive kinetic energy functionals based on the LMGP family of functionals; (2) adapting Quantum ESPRESSO’s implementation of rVV10 and vdW-DF nonlocal exchange-correlation functionals to be employed in sDFT simulations; (3) implementing “deorbitalized” meta GGA functionals (e.g., SCAN-L). We carefully assess the performance of the newly implemented tools on the S22-5 test set. eQE 2.0 delivers excellent interaction energies compared to conventional Kohn-Sham DFT and CCSD(T). The improved performance does not come at a loss of computational efficiency. We show that eQE 2.0 with nonlocal nonadditive functionals retains the same linear scaling behavior achieved in eQE 1.0 with semilocal nonadditive functionals.
Efficient DFT Solver for Nanoscale Simulations and Beyond (OE-SCF solver)
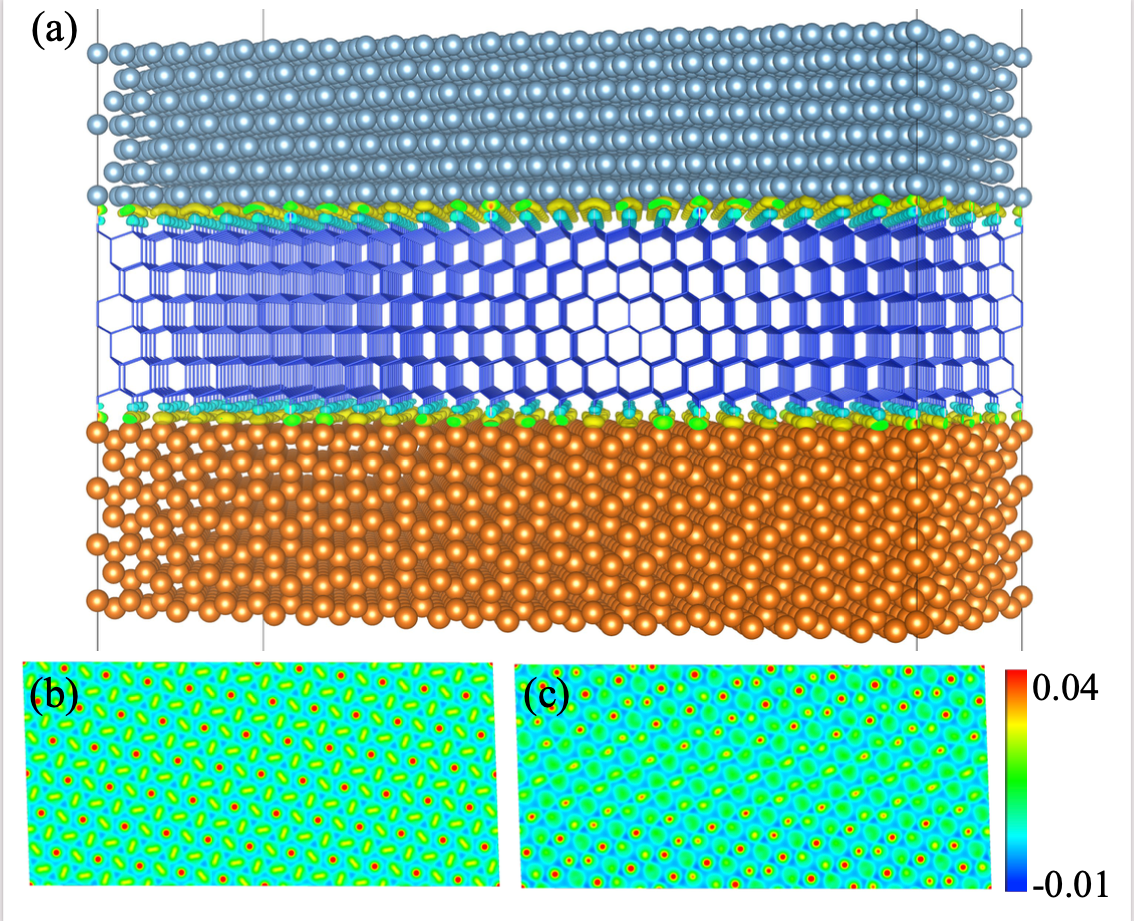
We present the one-orbital ensemble self-consistent field (OE-SCF), an alternative orbital-free DFT solver that extends the applicability of DFT to beyond nanoscale system sizes, retaining the accuracy required to be predictive. OE-SCF treats the Pauli potential as an external potential updating it iteratively, dramatically outperforming current solvers because only few iterations are needed to reach convergence. OE-SCF enabled us to carry out the largest ab initio simulations for silicon-based materials to date by employing only 1 CPU. We computed the energy of bulk-cut Si nanoparticles as a function of their diameter up to 16 nm, and the polarization and interface charge transfer when a Si slab is sandwiched between two metal slabs where lattice matching mandated a large contact area. Additionally, OE-SCF opens the door to adopting even more accurate functionals in orbital-free DFT simulations while still tackling large system sizes.
J. Phys. Chem. Lett. 12, 4134 (2021)
Nonlocal Subsystem Density Functional Theory
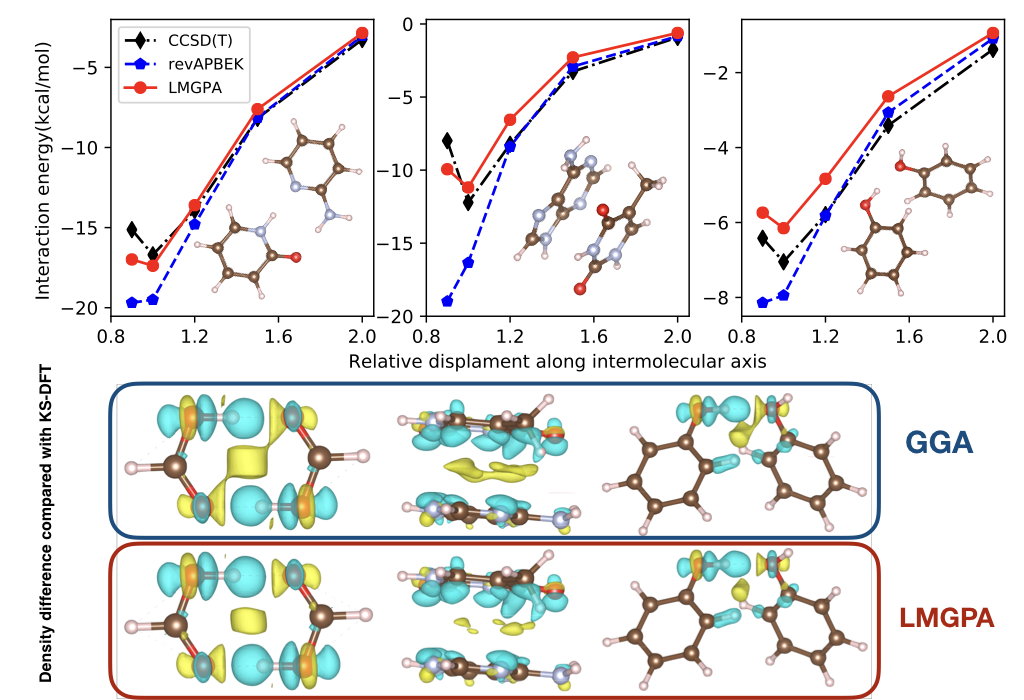
By invoking a divide-and-conquer strategy, subsystem DFT dramatically reduces the computational cost of large-scale, ab initio electronic structure simulations of molecules and materials. The central ingredient setting subsystem DFT apart from Kohn–Sham DFT is the nonadditive kinetic energy functional (NAKE). Currently employed NAKEs are at most semilocal (i.e., they only depend on the electron density and its gradient), and as a result of this approximation, so far large-scale simulations only included systems composed of weakly interacting subsystems. In this work, we advance the state-of-the-art by introducing fully nonlocal NAKEs in subsystem DFT simulations for the first time. A benchmark analysis based on the S22-5 test set shows that nonlocal NAKEs considerably improve the computed interaction energies and electron densities compared to commonly employed GGA NAKEs, especially when increasing intersubsystem electron density overlap is considered. Most importantly, we resolve the long-standing problem of too attractive interaction energy curves typically resulting from the use of GGA NAKEs.
J. Phys. Chem. Lett. 11, 272 (2020)
LMGP Kinetic Energy Density Functional
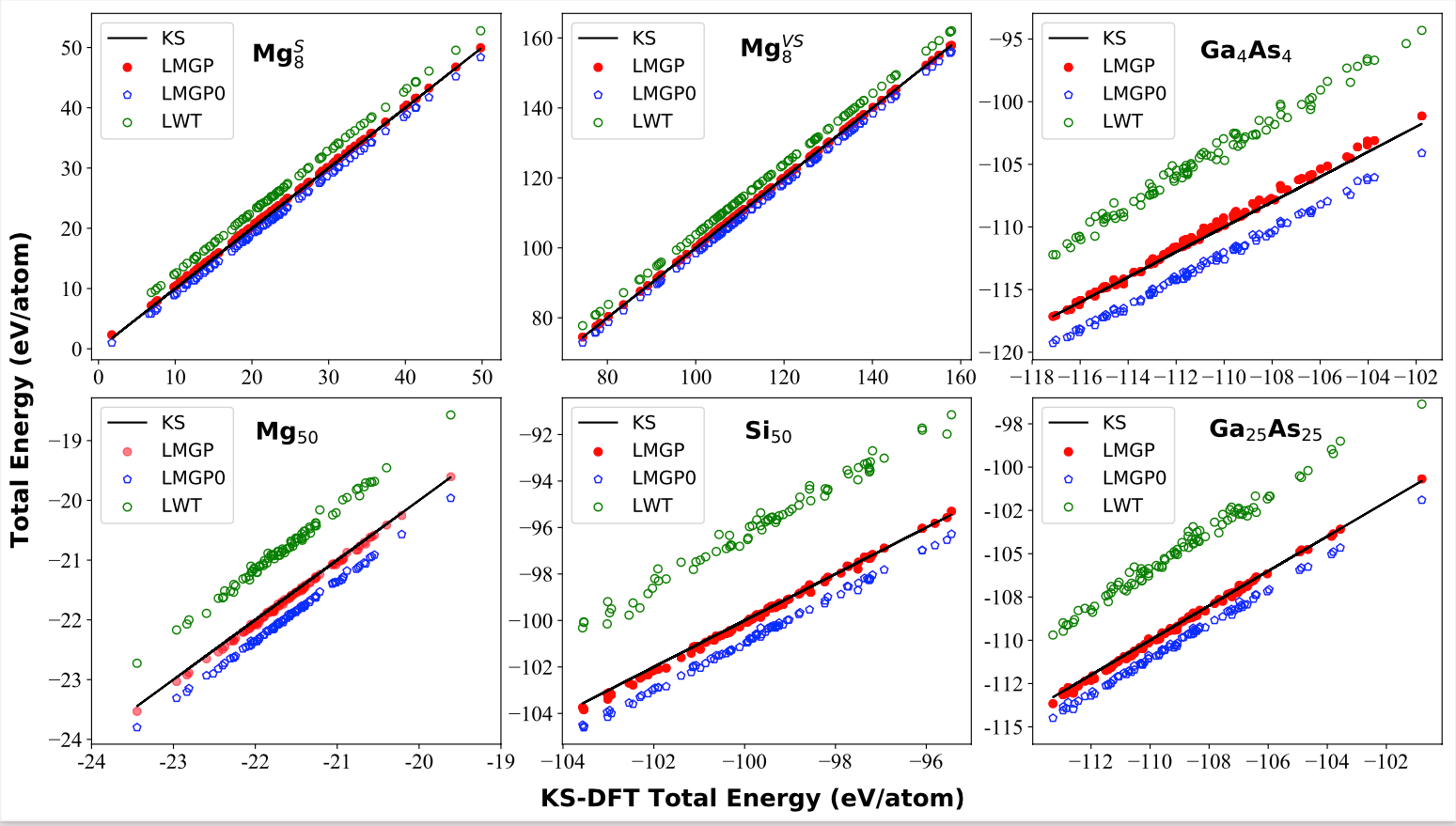
Million-atom quantum simulations are in principle feasible with orbital-free density functional theory (OF-DFT) because the algorithms only require simple functional minimizations with respect to the electron density function. In this context, OF-DFT has been useful for simulations of warm dense matter, plasma, cold metals, and alloys. Unfortunately, systems as important as quantum dots and clusters (having highly inhomogeneous electron densities) still fall outside OF-DFT’s range of applicability. In this Rapid Communication, we make considerable progress in addressing this century old problem by devising and implementing an accurate, transferable, and universal family of nonlocal noninteracting kinetic energy density functionals that feature correct asymptotics and can handle highly inhomogeneous electron densities. We show that OF-DFT achieves close to chemical accuracy for the electronic energy and reproduces the electron density to about 5% of the benchmark for semiconductor quantum dots and metal clusters. Therefore, this work shows that OF-DFT can reliably simulate systems with highly inhomogeneous electron density, such as clusters and quantum dots, with applicability to the rational design of materials.
Phys. Rev. B 100,041105(R) (2019)
Mi-Genova-Pavanello (MGP) Kinetic Energy Density Functional
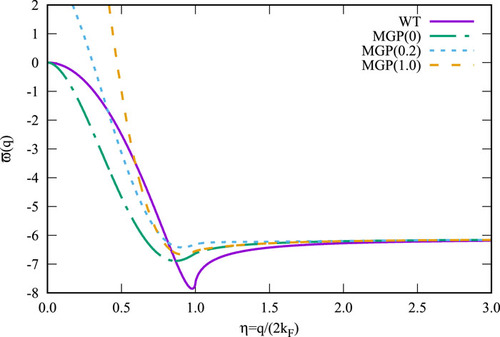
MGP is constructed to satisfy three exact conditions: (1) a nonzero “Kinetic electron” arising from a nonzero exchange hole; (2) the second functional derivative must reduce to the inverse Lindhard function in the limit of homogenous densities; (3) the potential is derived from functional integration of the second functional derivative. Pilot calculations show that MGP is capable of reproducing accurate equilibrium volumes, bulk moduli, total energy, and electron densities for metallic (body-centered cubic, face-centered cubic) and semiconducting (crystal diamond) phases of silicon as well as of III-V semiconductors
J. Chem. Phys. 148, 184107 (2018)
First-principle optimal local pseudopotentials (OEPP)
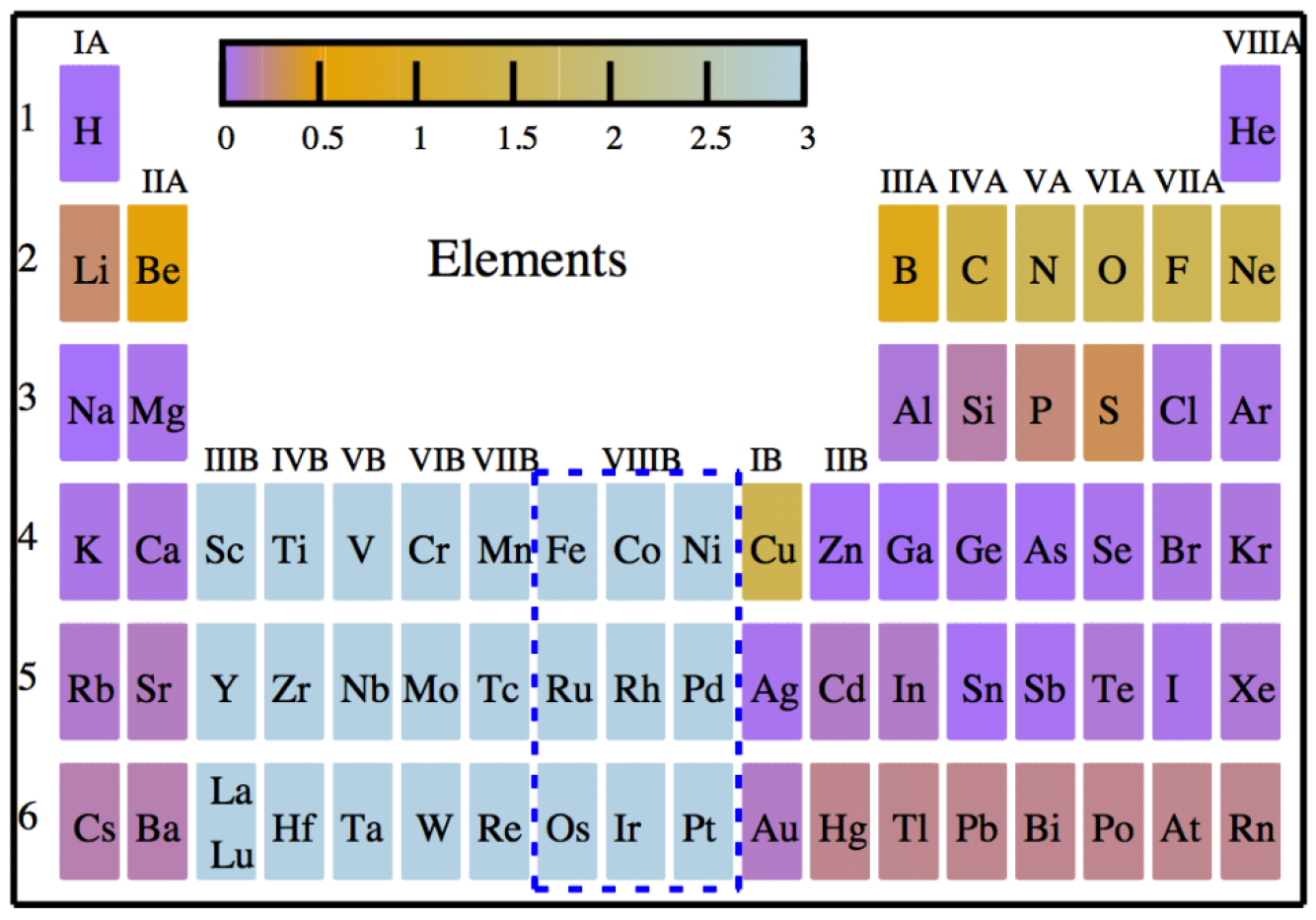
The local pseudopotential (LPP) is an important component of orbital-free density functional theory, a promising large-scale simulation method that can maintain information on a material’s electron state. The LPP is usually extracted from solid-state density functional theory calculations, thereby it is difficult to assess its transferability to cases involving very different chemical environments. Here, we reveal a fundamental relation between the first-principles norm-conserving pseudopotential (NCPP) and the LPP. On the basis of this relationship, we demonstrate that the LPP can be constructed optimally from the NCPP for a large number of elements using the optimized effective potential method. Specially, our method provides a unified scheme for constructing and assessing the LPP within the framework of first-principles pseudopotentials. Our practice reveals that the existence of a valid LPP with high transferability may strongly depend on the element.
J. Chem. Phys. 144, 134108 (2016)
Linear scaling method to evaluate the ion–electron potential of crystalline solids
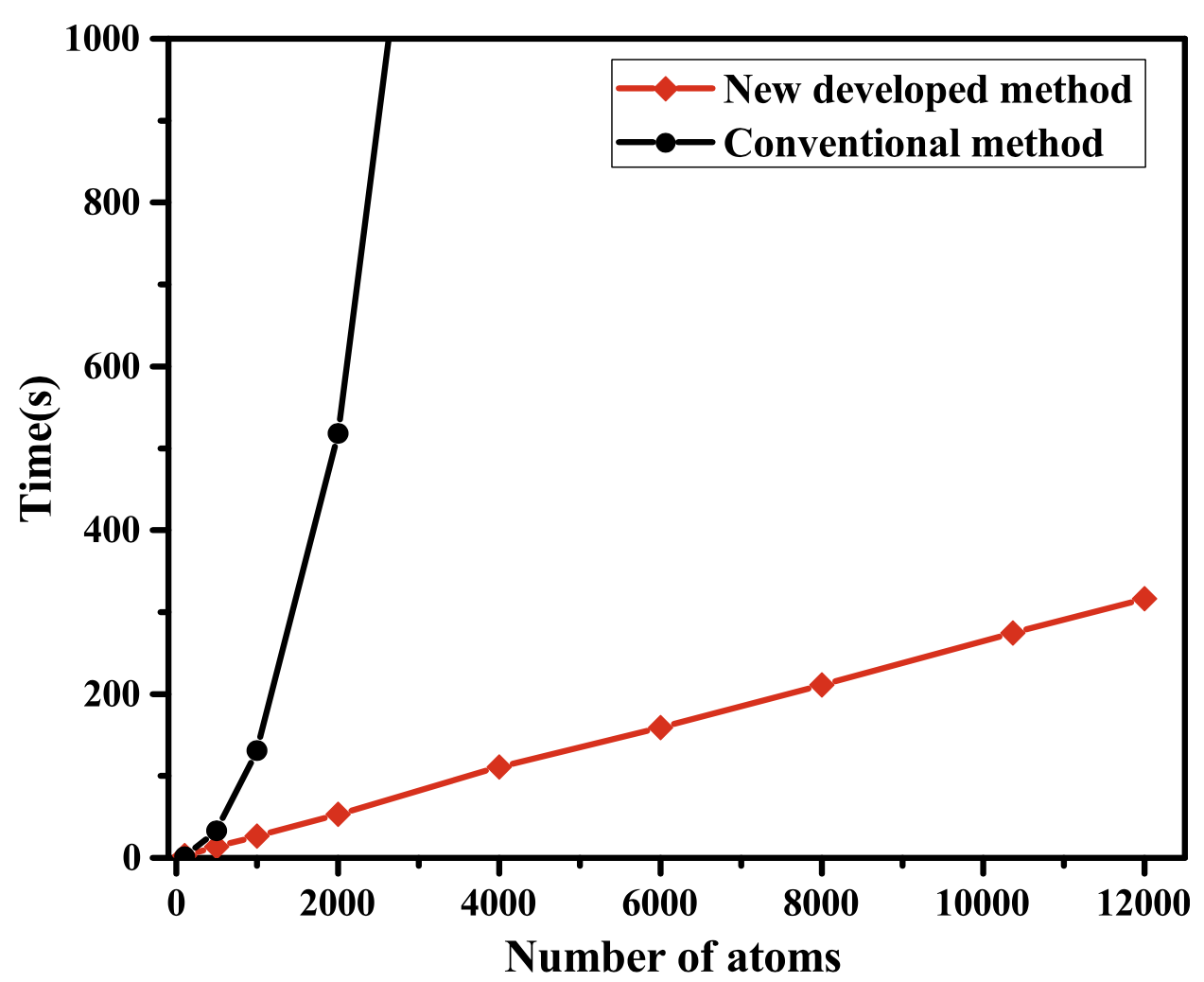
We propose a simple linear scaling expression in reciprocal space for evaluating the ion–electron potential of crystalline solids. The expression replaces the long-range on-electron potential with an equivalent localized charge distribution and corresponding boundary conditions on the unit cell. Given that no quadratic scaling structure factor is required—as used in traditional methods—the expression shows the inherent linear behavior, and is well suited to simulating large-scale systems within orbital-free density functional theory. The scheme is implemented in the ATLAS software package and benchmarked by using a solid Mg body-centered cubic lattice containing tens of thousands of atoms in the unit cell. The test results show that the method can efficiently simulate large scale crystals with high computational accuracy.
